Tag: if then

‘IF THEN’ with AI

Posted on by lechuck park

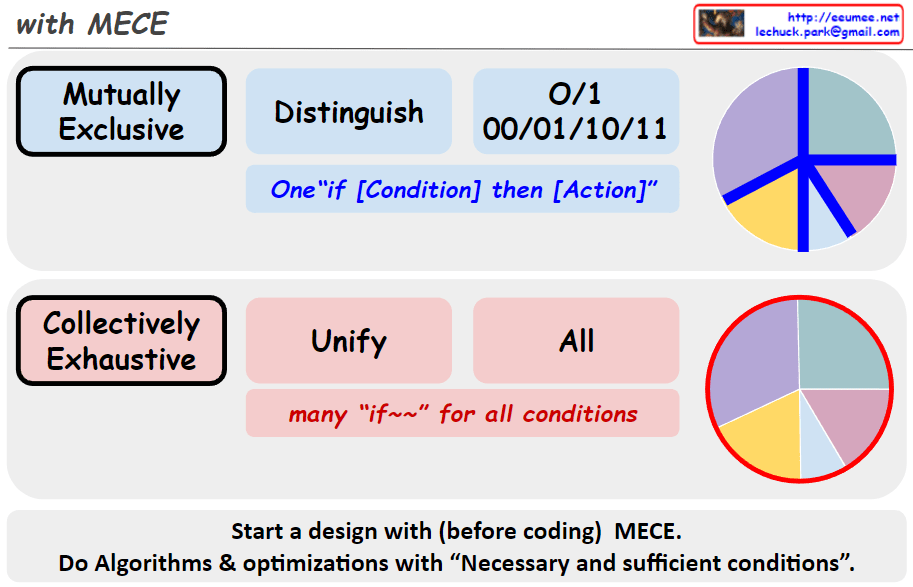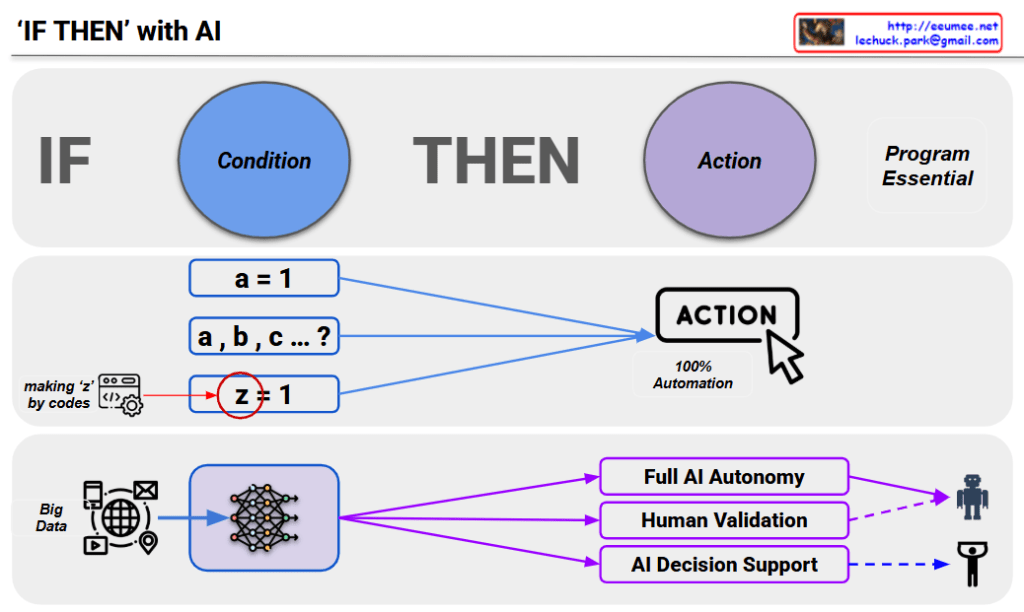
This image is a diagram titled “IF-THEN with AI” that explains conditional logic and automation levels in AI systems.

Top Section: Basic IF-THEN Structure

  • IF (Condition): Conditional part shown in blue circle
  • THEN (Action): Execution part shown in purple circle
  • Marked as “Program Essential,” emphasizing it as a core programming element

Middle Section: Evolution of Conditional Complexity

AI is ultimately a program, and like humans who wanted to predict by sensing data, making judgments, and taking actions based on those criteria. IF-THEN is essentially prediction – the foundation of programming that involves recognizing situations, making judgments, and taking actions.

Evolution stages of data/formulas:

  • a = 1: Simple value
  • a, b, c … ?: Processing multiple complex values simultaneously
  • Z ≠ 1: A condition that finds the z value through code on the left and compares it to 1 (highlighted with red circle, with annotation “making ‘z’ by codes”)

Now we input massive amounts of data and analyze with AI, though it has somewhat probabilistic characteristics.

Bottom Section: Evolution of AI Decision-Making Levels

Starting from Big Data through AI networks, three development directions:

  1. Full AI Autonomy: Complete automation that evolved to “Fine, just let AI handle it”
  2. Human Validation: Stage where humans evaluate AI judgments and incorporate them into operations
  3. AI Decision Support: Approach where humans initially handle the THEN action

Key Perspective: While these three development directions exist, there’s a need for judgment regarding decisions based on the quality of data used in analysis/judgment. This diagram shows that it’s not just about automation levels, but that data quality-based reliability assessment is a crucial consideration.

Summary

This diagram illustrates the evolution from simple conditional programming to complex AI systems, emphasizing that AI fundamentally operates on IF-THEN logic for prediction and decision-making. The key insight is that regardless of automation level, the quality of input data remains critical for reliable AI decision-making processes.

With Claude

“if then” by AI

Posted on by lechuck park

From Claude with some prompting
This image titled “IF THEN” by AI illustrates the evolution from traditional programming to modern AI approaches:

  1. Upper section – “Programming”: This represents the traditional method. Here, programmers collect data, analyze it, and explicitly write “if-then” rules. This process is labeled “Making Rules”.
    • Data collection → Analysis → Setting conditions (IF) → Defining actions (THEN)
  2. Lower section – “AI”: This shows the modern AI approach. It uses “Huge Data” to automatically learn patterns through machine learning algorithms.
    • Large-scale data → Machine Learning → AI model generation

Key differences:

  • Traditional method: Programmers explicitly define rules
  • AI method: Automatically learns patterns from data to create AI models that include basic “if-then” logic

The image effectively diagrams the shift in programming paradigms. It demonstrates how AI can process and learn from massive datasets to automatically generate logic that was previously manually defined by programmers.

This visualization succinctly captures how AI has transformed the approach to problem-solving in computer science, moving from explicit rule-based programming to data-driven, pattern-recognizing models.

MECE

Posted on by lechuck park

From DALL-E with some prompting
The image provides a visual explanation of design and algorithm optimization strategies based on the MECE principle, which stands for “Mutually Exclusive, Collectively Exhaustive.”

  • In the blue area at the top (“Mutually Exclusive”), there’s content related to “Distinguish,” which signifies conditions that are clearly differentiated from one another. It includes binary code formats “0/1” and “00/01/10/11” as examples, representing distinct states. The pie chart beside it illustrates segments that are clearly separated, denoting distinct categories. Below is the phrase “One ‘if [Condition] then [Action]'”, suggesting that for a specific condition, one action is defined—akin to an “if” statement in programming.
  • In the pink area at the bottom (“Collectively Exhaustive”), there’s content related to “Unify.” This implies the inclusion of all possibilities by using many “if~” statements for all conditions. The word “All” emphasizes encompassing and including every condition. The circular chart beside it shows various pieces coming together to complete a circle, representing completeness when all parts are combined.

The overall context suggests applying the MECE principle in programming or system design to distinctly separate mutually exclusive conditions (as shown in the top blue area) and to comprehensively address all possible conditions (as indicated in the bottom pink area) to ensure the entire system or program functions comprehensively. The statement “Start a design with (before coding) MECE. Do Algorithms & optimizations with ‘Necessary and sufficient conditions’.” advises to apply the MECE principle when starting a design and to consider necessary and sufficient conditions when working on algorithms and optimizations.