Tag: speed

Transmission Rate vs Propagation Speed

Posted on by lechuck park

Key Concepts

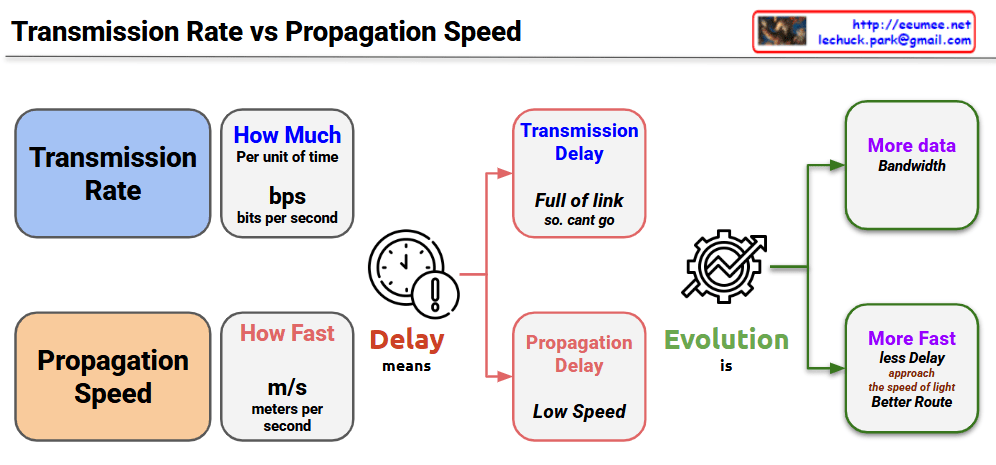
Transmission Rate

  • Amount of data processable per unit time (bps – bits per second)
  • “Processing speed” concept – how much data can be handled simultaneously
  • Low transmission rate causes Transmission Delay
  • “Link is full, cannot send data”

Propagation Speed

  • Speed of signal movement through physical media (m/s – meters per second)
  • “Travel speed” concept – how fast signals move
  • Slow propagation speed causes Propagation Delay
  • “Arrives late due to long distance”

Meaning of Delay

Two types of delays affect network performance through different principles. Transmission delay is packet size divided by transmission rate – the time to push data into the link. Propagation delay is distance divided by propagation speed – the time for signals to physically travel.

Two Directions of Technology Evolution

Bandwidth Expansion (More Data Bandwidth)

  • Improved data processing capability through transmission rate enhancement
  • Development of high-speed transmission technologies like optical fiber and 5G
  • No theoretical limits – continuous improvement possible

Path Optimization (More Fast, Less Delay)

  • Faster response times through propagation delay improvement
  • Physical distance reduction, edge computing, optimal routing
  • Fundamental physical limits exist: cannot exceed speed of light (c = 3×10⁸ m/s)
  • Actual media is slower due to refractive index (optical fiber: ~2×10⁸ m/s)

Network communication involves two distinct “speed” concepts: Transmission Rate (how much data can be processed per unit time in bps) and Propagation Speed (how fast signals physically travel in m/s). While transmission rate can be improved infinitely through technological advancement, propagation speed faces an absolute physical limit – the speed of light – creating fundamentally different approaches to network optimization. Understanding this distinction is crucial because transmission delays require bandwidth solutions, while propagation delays require path optimization within unchangeable physical constraints.

With Claude