Tag: mece

STEP BY STEP

Posted on by lechuck park

This image depicts a problem-solving methodology diagram titled “STEP by STEP.”

The diagram illustrates an efficient step-by-step approach to problem solving:

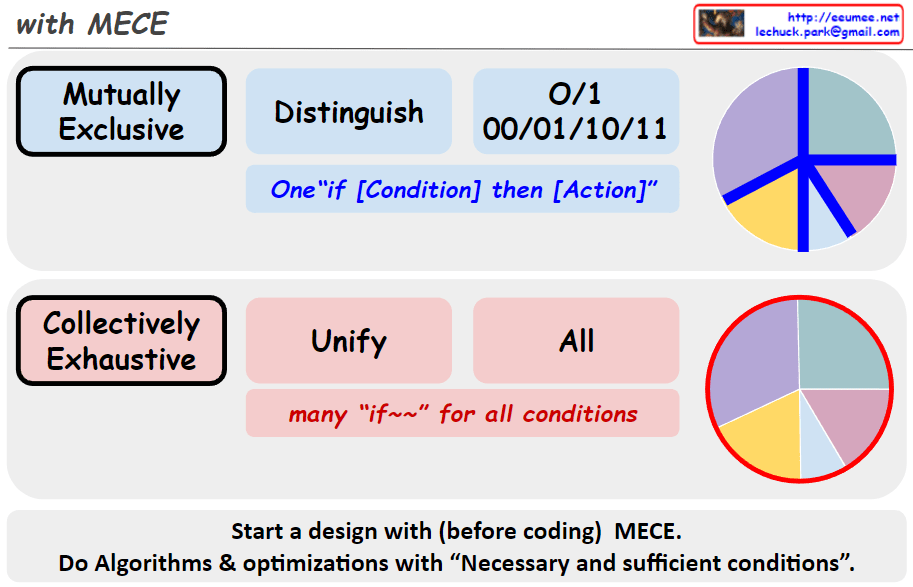
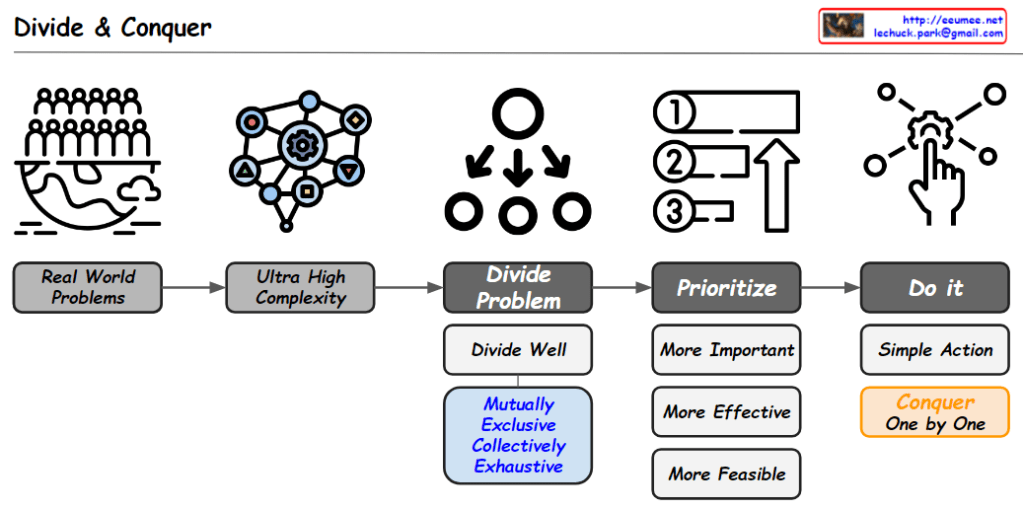
  1. “Do It First!! (Confirmation)” – This initial stage focuses on the fundamental and easy-to-solve portions (80%). The approach here emphasizes “Divide and conquer with MECE” (Mutually Exclusive, Collectively Exhaustive), “Logicalization,” and “Digitalization” as key perspectives for tackling problems.
  2. The second “DO IT” stage – This addresses the more complex portions (20%) and applies the same methodology used in the first stage.
  3. The third “DO IT” stage – This continues applying the methodologies from previous stages in an iterative process.

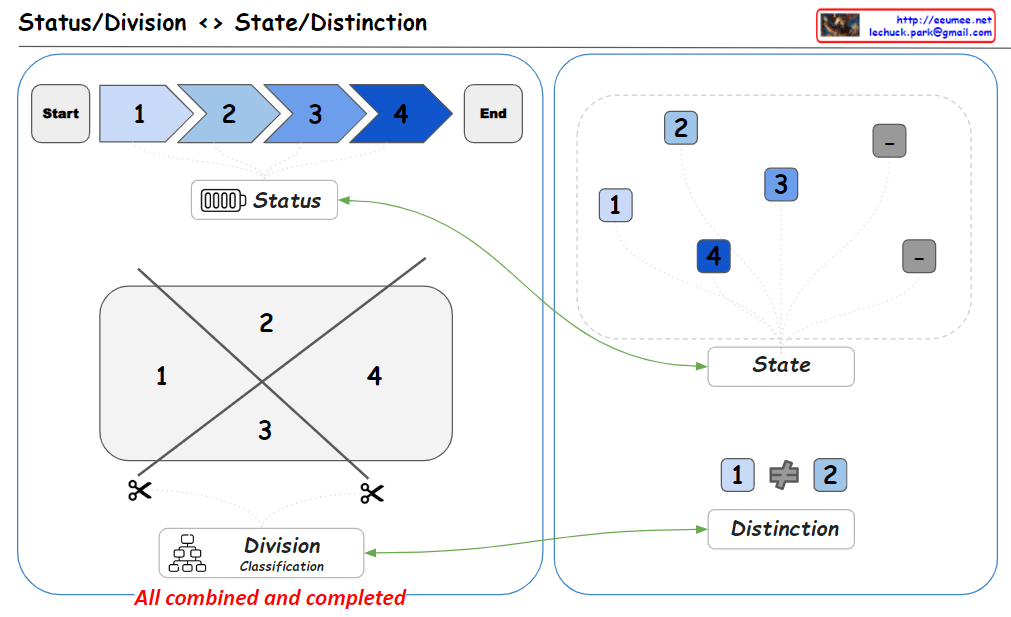
Each stage is divided into a 20% (blue) and 80% (green) ratio, demonstrating the application of the Pareto principle (80/20 rule). This suggests a strategy of first resolving the fundamental 80% of problems that are easier to solve, then approaching the more complex 20% using the same methodology.

The circular nodes and arrows at the top represent the progression of this sequential problem-solving process, with the red target icon in the upper left symbolizing the ultimate goal.

This methodology emphasizes a systematic approach to complex problems by breaking them down, addressing them logically, and digitalizing when necessary for efficient resolution.

With Claude

MECE

Posted on by lechuck park

From DALL-E with some prompting
The image provides a visual explanation of design and algorithm optimization strategies based on the MECE principle, which stands for “Mutually Exclusive, Collectively Exhaustive.”

  • In the blue area at the top (“Mutually Exclusive”), there’s content related to “Distinguish,” which signifies conditions that are clearly differentiated from one another. It includes binary code formats “0/1” and “00/01/10/11” as examples, representing distinct states. The pie chart beside it illustrates segments that are clearly separated, denoting distinct categories. Below is the phrase “One ‘if [Condition] then [Action]'”, suggesting that for a specific condition, one action is defined—akin to an “if” statement in programming.
  • In the pink area at the bottom (“Collectively Exhaustive”), there’s content related to “Unify.” This implies the inclusion of all possibilities by using many “if~” statements for all conditions. The word “All” emphasizes encompassing and including every condition. The circular chart beside it shows various pieces coming together to complete a circle, representing completeness when all parts are combined.

The overall context suggests applying the MECE principle in programming or system design to distinctly separate mutually exclusive conditions (as shown in the top blue area) and to comprehensively address all possible conditions (as indicated in the bottom pink area) to ensure the entire system or program functions comprehensively. The statement “Start a design with (before coding) MECE. Do Algorithms & optimizations with ‘Necessary and sufficient conditions’.” advises to apply the MECE principle when starting a design and to consider necessary and sufficient conditions when working on algorithms and optimizations.